Ultimate Stem by Marianna Jennings

Marianna Jennings is Chicago Public School high school math teacher with National Board Certification in AYA math. Marianna holds two masters degrees: one in Human Development and Learning and another in Curriculum and Instruction. Marianna is also a CPS Framework Specialist and has been teaching for 28 years.
Our Top 5 components
Creative teacher designed lessons encourage outcomes that draw out student’s strengths
Teachers use real world situations and tools that engage students to connect to their own world
Hands on learning.
Students develop their own evidence which leads to relational understanding. “I hear and I forget. I see and I remember. I do and I understand.” (Confucius)
Communication/Collaboration
Student discussions in various groupings allow students to drive the lesson and take ownership of their learning by sharing their interpretations and giving feedback.
Open ended
There is not one right answer. Lessons direct students to articulate concepts in their own words and/or provide their own examples or creative responses.
Multiple access points for students to succeed
Students with varying ability levels can collaborate with peers and meaningfully contribute to the their group’s success. Multiple intelligences are addressed in each lesson
Creative teacher designed lessons encourage outcomes that draw out student’s strengths
Teachers use real world situations and tools that engage students to connect to their own world
Hands on learning.
Students develop their own evidence which leads to relational understanding. “I hear and I forget. I see and I remember. I do and I understand.” (Confucius)
Communication/Collaboration
Student discussions in various groupings allow students to drive the lesson and take ownership of their learning by sharing their interpretations and giving feedback.
Open ended
There is not one right answer. Lessons direct students to articulate concepts in their own words and/or provide their own examples or creative responses.
Multiple access points for students to succeed
Students with varying ability levels can collaborate with peers and meaningfully contribute to the their group’s success. Multiple intelligences are addressed in each lesson
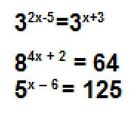
Trading Places: Exponential Equality
This lesson transformed direct instruction into one that allowed the student to take ownership of their learning and through conversation and collaboration explored a concept. I deliberately placed students into groups which were comprised of varied learners. They are introduced to a concept that they are attempting to discover. In this case, the concept was exponential equality. I then carefully chose problems that are scaffolded. The students worked in groups on the problems (one problem at a time).
Students wrote down their insights and generalizations about how they progressed from equation to equation. Students then shared with their small group and then in a large group discussion. The goal was for students to be working toward the understanding that if the bases were the same, then the exponents would be the same. The following problems were then given to challenge their generalizations by ramping up the level of difficulty.
This lesson transformed direct instruction into one that allowed the student to take ownership of their learning and through conversation and collaboration explored a concept. I deliberately placed students into groups which were comprised of varied learners. They are introduced to a concept that they are attempting to discover. In this case, the concept was exponential equality. I then carefully chose problems that are scaffolded. The students worked in groups on the problems (one problem at a time).
Students wrote down their insights and generalizations about how they progressed from equation to equation. Students then shared with their small group and then in a large group discussion. The goal was for students to be working toward the understanding that if the bases were the same, then the exponents would be the same. The following problems were then given to challenge their generalizations by ramping up the level of difficulty.
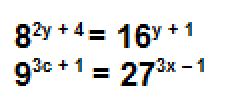
After these two problems, groups were asked to create their own formal representation of exponential equality using only variables. One group member from each group wrote it on the board. During the whole group discussion, we looked for similarities in the representations.
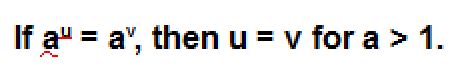
As an exit ticket, students wrote their own problem. This exit ticket served as a quick formative assessment. These problems were used in class the next day for reinforcement.
This lesson was powerful because it asked students to collaborate and draw conclusions. I asked the students to reflect individually by writing their first generalizations and then as a group on the final representations. I felt that the lesson was driven by the students. I listened to their conversations and then adapted my guidance to their needs. I designed the lesson to specifically allow students to confront common mistakes or misconceptions about exponents and figure out why they were mistakes (for example: 64 = 8 x 8 so students might think it is 8 raised to the 8th power). Students took ownership for their learning while I learned more about how they think and process the math concept.
This lesson was powerful because it asked students to collaborate and draw conclusions. I asked the students to reflect individually by writing their first generalizations and then as a group on the final representations. I felt that the lesson was driven by the students. I listened to their conversations and then adapted my guidance to their needs. I designed the lesson to specifically allow students to confront common mistakes or misconceptions about exponents and figure out why they were mistakes (for example: 64 = 8 x 8 so students might think it is 8 raised to the 8th power). Students took ownership for their learning while I learned more about how they think and process the math concept.
